Studied CML
논문 : https://www.cs.cornell.edu/~ylongqi/paper/HsiehYCLBE17.pdf
0. Abstract
Metric Learning은 데이터 간 관계를 잘 나타내도록 임베딩한 결과 사이 관계(거리)를 학습하는 알고리즘을 의미한다. 본 논문에서 우리는 metric learning과 collaborative filtering 간의 연관성에 대해서 연구하였고, 그 결과
Collaborative Metric Learning(CML)이 탄생했다.
CML은 user의 선호도 (user-item) 뿐만 아니라 user-user, item-item 간의 유사도 역시 표현할 수 있는 metric space를 학습했다. CML은 기존 collaborative filtering 관련 sota 모델에서 성능을 뛰어넘었을 뿐만 아니라 Top-K recommendation task에서 nearest-neighbor search with negligibale accuracy reduction을 사용해서 엄청난 시간 단축을 보였다.
1. Introduction
Metric Learning

Distance는 KNN, Kmeans, SVM과 같은 많은 머신러닝 알고리즘에서 기초가 되는 개념이다. Metric learning algorithm은 데이터 간의 유사도를 잘 잡아 내는 distance metric을 생성한다. 이는 이미지 분류, 문서 복원, 단백질 함수 예측 등 태스크에서 필수적인 알고리즘이 되었다.
본 CML 논문에서는 metric learning이 collaborative filtering 문제에서 어떻게 적용되고, 여타 sota 모델들과 비교할 예정이다. Metric learning의 목표는 어떤 object pair가 similar한지 dissimilar한지를 잘 표현할 수 있는 distance metric을 만드는 것이다. 특히 우리는 similar pair간에는 가까운 위치에, dissimilar pair 간에는 멀게 위치하도록 하고 싶다. 예를 들어 face recognition에서 metric learning이 사용된다면 같은 사람의 사진은 가깝게, 다른 사람들의 사진은 멀게 embedding되는 알고리즘을 학습하게 된다.
Triangle Inequality

수학적으로 metric은 여러 조건을 충족해야 하는데, 이 중 triangle inequality가 일반화할 때 가장 중요한 문제가 된다. Triangle inequality란 세 개의 object가 있을 때, 두 pairwise 거리의 합은 남은 하나의 거리보다 길어야 한다는 것이다. (삼각형 결정 조건 : 길이가 가장 긴 변의 길이는 다른 두 변 길이의 합보다 작아야 삼각형을 그릴 수 있다)
(x, z): d(y, z) ≤ d(x, y) + d(x, z).
이를 recommmender system에 적용해보면, x가 y랑 z와 가까워질 때 learned metric은 (x, y) (x, z)를 가깝게 만들 뿐만 아니라, (y,z)도 상대적으로 가까워질 가능성이 높아진다. 이렇듯, 아직 우리가 정의하지 못한 (y,z)에도 x와의 각각의 관계를 보고 '유사하다'고 보며 영향을 주는 과정을 논문에서는 “similarity propagation” process라고 불렀다. learned metric가 주어진 다른 정보들로 모르는 정보까지 영향을 주게 되는 것이다.
이 유사도 전파(similarity propagation)은 CF와 긴밀하게 연관되어 있다. 유사도 전파가 보지 못한 pair (y,z)에 영향을 주듯, Collaborative Filtering에서도 user과 item의 latent vector를 가지고 아직 보지 못한 user-item pair에도 일반화하려고 하기 때문이다. matrix factorization의 경우 user-item vector간의 내적 값으로 known rating을 학습하고, 그 결과로 얻은 vector간 내적으로 새로운 rating을 예측하기 때문이다.
Matrix factorization과 metric learning은 개념적으로 유사하지만 완전 같지는 않다. 왜냐하면 dot product는 매우 중요한 triangle inequality 정의를 성립하고 있지 않기 때문이다. Matrix factorization은 user의 general한 관심사(interest)를 학습할 수는 있어도, triangle inequality가 성립되지 않으면 선호 정보를 정확히 표현하지 못할 수도 있다. 또한 기존 matrix factorization알고리즘들은 user-user과 item-item 간의 관계를 표현하는데 한계가 있었다.
본 논문에서는 user 선호뿐만 아니라 user-user, item-item간의 유사도 역시 학습한 CML을 소개한다. 우리는 implicit feedback dataset에 집중했고, CML은 다양한 추천 도메인에서 기존 SOTA 모델을 압도하는 성능을 보임을 보여줄 것이다. CML의 contribution은 user의 내재된 선호도 파악했다는 것이다. Flickr photographic dataset에서 user의 내재된 선호를 파악해 추천해주는 모습을 보였다. 또한 CML은 image, text, tag 등 다양한 item feature를 복합적으로 파악했다. 마지막으로 CML은 Top-K recommendation 태스크에서 매우 빠르면서도 정확한 성능을 보여주었다.
2. Background
2장에서는 Metric learning, LMNN, CF의 개념들에 대해서 알아볼 예정이다.
2.1. Metric Learning
Metric learning에서 사용하는 대표적인 거리 함수로는 Mahalanobis 거리 공식이 있다. 유클리드 거리공식과의 차이는, Mahalanobis 거리 공식은 전체적인 데이터 분포를 반영한다는 점이다.

위의 식은 Mahalanobis 거리 공식이다. 이를 distance function이라는 의미로 d라고 표기한다.
A는 m x m 사이즈의 positive semi-definite matrix 다.
출처 : https://ko.wikipedia.org/wiki/정부호_행렬
positive semi-definite matrix (양의 정준부호 행렬) : 모든 고윳값이 음수가 아닌 경우 (즉, 0이 아닌 모든 벡터 x에 대해 x * Mx ≥ 0인 경우) M은 양의 준정부호 행렬(영어 positive semi-definite matrix)

가장 일반적으로 거리를 최소화하는 수식(global optimization)을 짜면 다음과 같다.
위의 식에서 S 집합은 특성이 비슷한 item i, item j를 의미하고, D 집합은 dissimilar 즉 비슷하지 않은 item i, item j를 의미한다.
따라서 위 식을 해석하면 S 즉 similar한 아이템들의 거리는 최소화하고
D에서 나온 item i랑 item j의 거리는 최소 1이상이어야 하며, A는 양의 준정부호행렬을 가정한다.
2.2. Metric Learning for kNN
2.1.에서 다루었던 global optimization은 모든 비슷한 pair은 당기고, 모든 dissimilar pair은 밀어내는 distance metric을 학습한다. 하지만 이 목적인 모든 경우에 가능한 것은 아니다.
반면, Weinberger은 논문 “Distance metric learning for large margin nearest neighbor classification” 일명 LMNN에서 k-nearest neighbor classification에서 이 metric을 사용하면 훨씬 학습 효율이 좋아진다는 것을 증명했다. 이는 달성하기 훨씬 쉽고, 우리도 모델에 적용하기로 했다.
LMNN 논문 링크 : https://jmlr.csail.mit.edu/papers/volume10/weinberger09a/weinberger09a.pdf
우리가 많이 참고한 이 논문에서 소개된 LMNN의 loss function에 대해서 설명하려고 한다.
LMNN에서 인풋은 x라고 정의한다. 우리는 x와 가까울 것으로 기대하는 같은 클래스 data point들을 “target neighbors”라고 정의한다.
x 주변으로 형성된 target neighbor들은 특정 둘레( perimeter )를 만드는데, 이 둘레 내에는 다른 레이블인 데이터 포인트가 침범해서는 안되는 공간으로 간주된다. x와 다른 클래스면서 둘레 내에 위치해, 침범하고 있는 포인트들은 “imposters”라고 부른다.

위의 그림을 보면 명확해진다. 가운데 xi가 있고, 같은 클래스는 노란색으로 지정된다. 이 노란색 데이터는 "target neighbors"라고 부른다. 그리고 다른 색깔로 그려진 dissimilar 데이터 포인트들은 "imposters"라고 부른다.
LMNN은 이 둘레 내의 imposters 개수가 적어지도록 학습하는 metric을 학습하려고 한다.

LMNN의 loss function은 두 가지 파트로 나뉘어있다. Pull loss, Push loss 위의 식은 원 논문에서 표현된 식이다.
먼저 pull loss부터 알아본다.

pull loss는 간단한 거리 공식을 최소화하는 loss이다. j~i라는 기호는 j가 i의 target neighbor라는 뜻이다. 따라서 수식을 해석하면 i와 target neighbor인 pair에 대해서 d() 거리 함수를 줄이는 loss임을 알 수 있다.
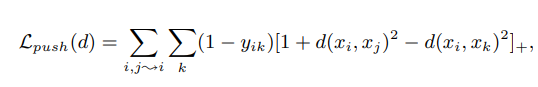
다음은 push loss이다. push loss는 imposter과의 거리를 멀어지는 것을 목표로 한다.
여기서 i, j는 similar item들이고 k는 imposter라고 한다. d(xi, xj)의 거리 제곱은 우리가 줄이고자 하는 distance이고, d(xi, xk)는 우리가 늘리고자 하는 distance이다. 따라서 d(i j) - d(i k)를 뺐을 때 값이 작으면 좋은 것이다.
결과에 []+인 max(x, 0)이 되어서 안의 값이 마이너스면 0이 된다. 커지면 그 값을 그대로 활용한다.
(1- y)에서 y는 imposter k가 다른 클래스일 때 0, 같은 클래스일 때 1의 값을 가지므로 다른 클래스일때만 해당 loss를 사용하는 것을 알 수 있다.
2.3. Collaborative Filtering
전통적인 협업 필터링은 cosine similiarity와 같은 heuristics로 user similarity를 측정했다.
그리고 최근에는 matrix factorization (MF)가 각광받고 있다. original MF 모델은 user과 item을 latent factor space로 맵핑해서 그들의 숨겨진 feature를 내적으로 알아내는 방식을 취했다. 대표 loss function은 다음과 같다.
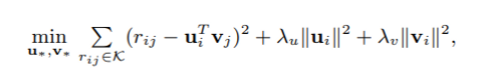
2.3.1. Implicit Feedback
Explicit feedback을 제외하고 user의 선호도를 확인하는 방법은 다양하다 : 북마크, 클릭 등, 이런 간접적인 선호 확인 방법을 implicit feedback이라고 할 수 있다.
Implicit feedback은 보통 explicit feedback보다 더 풍부하고, 편향이 적어서, 커뮤니티에서 많은 관심을 가지고 있다.
하지만 traditional matrix factorization으로는 implicit feedback은 적용하기 어려운데, 왜냐하면 우리는 오직 positive feedback만 남게 되기 때문이다. 우리는 unobserved 즉 관측되지 않는 user-item 관계를 단순히 negative하다고 치부할 수 없는게, 유저가 관심이 없을수도 있지만(true negative) 미처 발견을 못했을 문제도 있기 때문이다.
이 문제를 해결하기 위해 Hu와 Pan은 weighted regularized matrix factorization (WRMF)를 소개했고 이는 unobserved user item 관계를 negative하다고 보고, case weight C를 도입해서 불확실성의 영향을 줄이는 것이었다. case weight은 확실하게 있었던 feedback의 값이 크게 조정되어 loss function에 큰 영향을 주고, 아예 없었던 user-item interaction의 weight은 작게하여, 영향을 작게 만들었다.
2.3.2. Bayesian Personalized Ranking
더 나아가 최근 matrix factorization model들은 rating을 단순하게 예측하는 것에서 벗어나 이제 아이템 간의 선호 순서, 차이를 더 주목하기 시작했다. Bayesian personalized ranking (BPR)이 가장 대표적인 예시다.
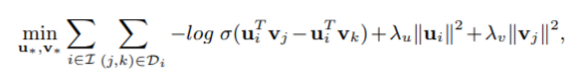
Di데이터셋에서 (j, k)조합은 i라는 유저가 j에게 feedback이 있었지만 k는 없었다는 의미다. (pair로 묶음)
이때 BPR은 i가 j를 k보다 선호한다고 받아들이고 위의 loss function을 만든다.
uivj 내적에서 uivk 내적을 빼고 sigmoid를 한 결과를 log를 취한다.
그리고 u, v의 절대값을 더하는 regularization 식을 추가한다.
-log sigmoid + regularization 결과를 최소화하는 것이 BPR의 목표다.
이 loss function을 통해 BPR은 predicting의 에러를 최소화하려고 한다. 이는 AUC curve를 최대화하는 것과 같은 효과를 가져온다. 하지만 BPR loss는 선호도가 낮은 아이템은 확실하게 밀어내지 않는다는 문제가 존재했다. 이는 Top-K recommendation task에서 문제가 있었다. 이 문제를 해결하기 위해 weighted ranking loss를 도입했다.
3. Collaborative metric learning
앞에서 논의했던 것처럼 최근 CF는 특정 유저가 이 아이템에 대해서 어떤 rating을 줄지 예측하는 것이 아니라 item들간의 상대적인 선호 차이를 알아내는 것을 목표로 삼고있다.
본 장에서는 CML이 이런 상대적인 관계를 어떻게 자연스럽게 알아낼 수 있는지 설명하려고 한다.
user-item pair S는 impliit feedback이 보였던 user-item 조합으로, positive feedback만 존재한다. 이를 활용해 비슷한 pair들은 가깝게 만들고, 상대적으로 다른 pair들은 멀리 떨어뜨리려고 한다. 이 과정에서 triangle inequality rule에 의해,
- 같은 아이템을 좋아한 유저들
- 비슷한 유저가 좋아했던 아이템들
을 클러스터링하려고 한다.
이렇게 되면 어떤 유저가 등장하든간에,
- 그 유저가 직전에 좋아했던 아이템들과
- 비슷한 취향을 가진 유저가 좋아했던 아이템
들로 nearest neighbor item들이 나올 것이다.
우리는 user-item pair뿐만 아니라 user-user item-item 관계도 반영해서 성능을 더 올릴 수 있었다.
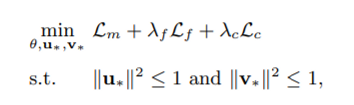
CML은 위의 loss function을 가지고 있다. Lm, Lf, Lc
각각에 대해 차례대로 알아보겠다.
3.1. Model formulation
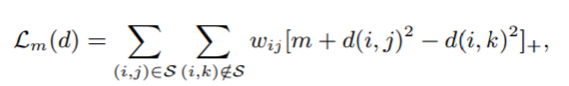
첫번째 loss는 metric loss(Lm)다.
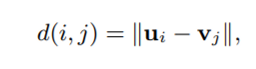
우리 모델은 user과 item vector을 각각 u, v로 표현할 것이다. (같은 dimension에 존재)
그리고 이 vector을 distance 함수로 계산한다. 만약 j를 선호하고 k를 선호하지 않는다면 위의 식에서 d(i, j)는 d(i, k)보다 작아야 한다. 만약 차이가 크면 0이 되어서 loss가 0이 되고 반대면 값이 커져, 줄여야 하는 대상이 된다.
m은 safety margin size다.
[x]+ 는 max(x, 0)
w는 ranking loss weight다. 이는 3.2 에서 설명된다.
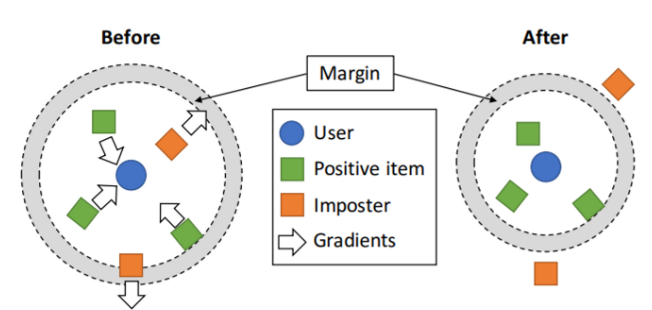
위 사진은 metric loss의 결과를 보여준다. 이 loss function은 LMNN과 유사하지만, 중요한 차이가 있다.
- L pull term이 없다. 왜냐하면 item은 많은 유저에게 좋아해질 수 있고 모든 유저에게 다 당겨지는 것이 현실적으로 가능하지 않기 때문이다. 하지만 push loss는 존재한다. push loss는 positive item을 유저에게 가깝게 만들기 때문이다.
- 우리는 Top-K recommendation을 개선하기 위해 weighted ranking loss를 도입했다.
3.2. Approximated Ranking Weight
위 metric loss에는 weightij가 있었다. 우리는 아이디어로 Weighted Approximate-Rank Pairwise(WARP) loss를 참고했다.
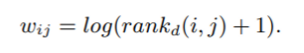
wij는 다음 식처럼 표현된다.
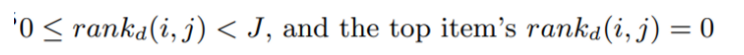
rankd(i, j)는 user i의 item j의 순위를 의미한다. 값은 0~J(J는 전체 아이템 개수를 의미) 가지며, 가장 높은 순위는 0의 값을 가진다.
우리는 positive item j를 rank에 따라 weight를 줄 수 있다. 이는 낮은 rank에 있는 positive item을 위에 있는 아이템보다 무겁게 처벌한다. 하지만 rank(i, j)를 각 graident descent step에서 계산하는 것은 연산 비용이 비싸다.
그래서 Weston은 “Distance metric learning with application to clustering with side-information”논문에서 negative item을 랜덤으로 샘플해서 비교하는 방법을 취했다.
N은 imposter k를 찾기 위한 negative items 집합이라고 하면, rank(i, j)는 [J / N ] 내림을 한 것 과 같은 값이 된다. 이는 object detection에서 사용했던 negative sample mining이랑 비슷한 과정이다. (논문 : Efficient sample mining for object detection
sample 횟수 U는 보통 10이나 20으로 설정해서 샘플하는 과정이 너무 길지 않도록 한다.
최신 GPU를 사용하면 병행하는 것이 가능해진다.
- 각 user-item pair(i, j) 마다 U개의 negative item을 병행하여 뽑는다. 그리고 처음 공식을 계산한다.
- M은 U 샘플에서 imposter개수를 의미한다. rank(i, j)는 이제 [J x M / U] 내림값이 된다.
매번 U개의 negative item을 샘플하는 것이 불필요해보일 수 있다.
하지만 우리는 CML이 epoch 몇 개만으로도 positive item을 훨씬 빠르게 high rank로 push하는 모습을 볼 수 있었다
3.3. Integrating Item Features
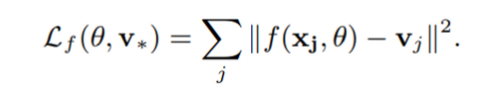
이번 장에서는 function loss를 알아볼 것이다. Transformation f는 raw feature를 우리가 원하는 latent space로 변환해주는 함수를 뜻한다.
theta Θ 는 f 함수의 파라미터를 의미한다. 그래서 f()는 f(xj , theta) 즉 인풋과 파라미터를 받는 함수로 정의할 수 있다. 이 f로 우리는 dropout이 있는 MLP(multi layer perceptron)을 사용할 것이다. 위의 L2 norm loss function은 f()를 Gaussian prior로 취급하게 된다.
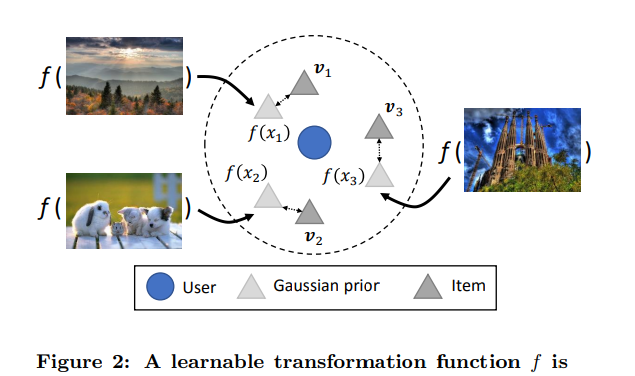
위의 그림처럼 f(x)는 item j의 raw feature를 넣은 MLP 함수의 결과를 의미하고, vj는 item의 vector를 의미한다.
우리는 vj에 대한 정보를 더 많이 알기 때문에 vj의 위치를 미세 조절하게 된다.
논문은 Lf와 Lm은 서로에게 영향을 준다고 했다. (mutually inform each other)
Lf는 user preference와 가까운 feature를 배울 수 있게 도와주고,
Lm은 비슷한 성격의 아이템들이 묶이도록 만들어 평가가 적은 아이템에 대해서도 잘 평가하도록 도와준다.
3.4. Regularization
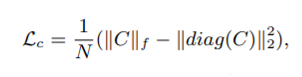
마지막 loss function은 covariance loss다.
Weight가 너무 큰 값을 가지게 되면 모델이 많이 복잡해지는데, 이러한 구불구불한 함수를 가지지 않도록 적절한 regularization이 필요하다. 우리가 제안하는 kNN 형태의 모델은 dimension이 너무 많으면 data point가 지나치게 멀어져서 효과적이지 않다. (curse of dimensionality)
다른 matrix factorization model과 달리 L2 norm을 사용하지 않는 점을 주목하자. l2 norm은 origin을 향해 모든 object를 당기는 성향이 있다. 이는 우리 모델과 같이 원점이 큰 의미가 없는 모델에서는 적용할 이유가 없게 된다.
우리가 사용한 regularization technique은 covariance regularization이다. 이는 “Reducing overfitting in deep networks by decorrelating representations”이라는 논문에서 제안되었다. Covariance regularization은 DNN에서 activation 간의 correlation을 줄이는데 사용되었다.
우리는 metric learning에서 dimension 간의 correlation을 줄이는데도 효과가 있다는 것을 발견했다.
yn을 object의 latent vector라고 할 때 (object는 user / item 둘다 가능)
n은 batch size N에서 object의 index를 의미한다.
Covariance를 적용하면 다음과 같다.
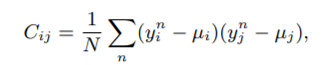
모든 dimension 간의 pair을 i, j라고 표현할 때 dimension간의 covariance는 Cij로 표현한다.
그리고 이 C를 convariance loss에 적용한 것이 아래 loss function
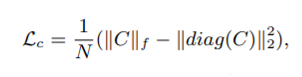
여기서 covariance에 사용된 norm은 Frobenius norm이다.
Covariance는 dimension 간 중복을 알아낼 수 있는 수단인만큼, 이 loss는 dimension이 중복되는 것을 막아주고, whole system을 주어진 메모리 내에서 효과적으로 표현하도록 유도해준다.
3.5. Training procedure
결론적으로 우리가 제안하는 모델은 세 가지 loss가 존재한다.
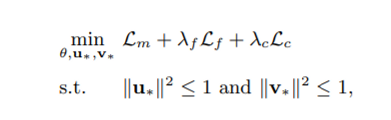
λ 람다는 모델을 학습할 때 우리가 줄 수 있는 하이퍼 파라미터로 각 loss term의 weight를 나타낸다.
우리는 이를 mini batch SGD로 줄이게 되고, learning rate control은 AdaGrad를 사용했다.
학습과정은 다음과 같다.
- sample N positive pairs from S
- Each pair, sample U negative items and rank
- for each pair keep item k that maximize hinge loss and form a mini batch of size N
- compute gradient and update parameter
- Censor norm u and v by y = y / max(||y||, 1)
- repeat until convergence
3.6. Relation to other models
이 자에서는 CML과 연관 있는 다른 모델에 대해 알아볼 예정이다.
CML은 BPR과 다른 MF 모델들과 많이 유사한데, traingle inequality에서 차이가 나는 점이 결정적인 차이를 만든다.
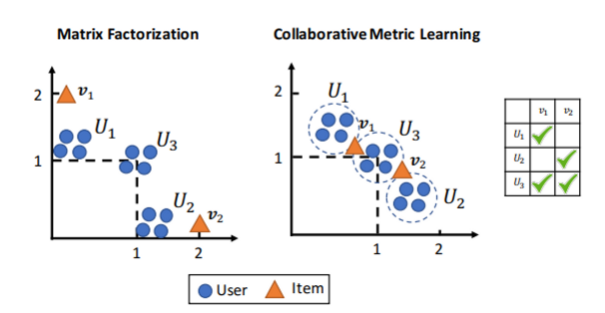
논문에 실린 Figure 3은 위의 그림과 같다. 맨 오른쪽 그림처럼 u1, u2, u3의 v1, v2에 대한 선호가 있다고 할 때, 선호한 아이템은 ‘2’로 관심 없던 item에 대한 선호를 ‘0’으로 값을 지정하고 matrix factorization을 만들면 다음과 같다.
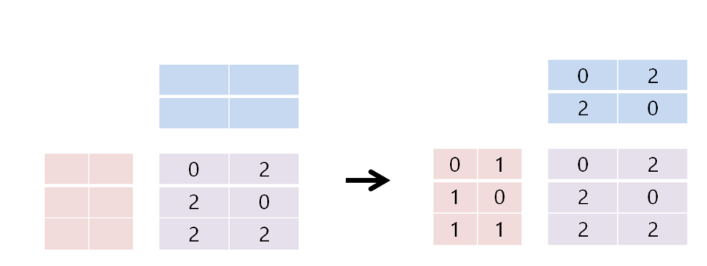
이 0,2,2,0,2,2 matrix로 user latent vector과 item latent vector를 만들면 오른쪽과같다.
각 user, item을 보면 user는 자기 선호대로 잘 나온 것 같고, 내적하면 각 칸에 맞는 값이 나오니까 잘 나온 것처럼 보이지만 논문은 u3에 대한 정보가 제대로 표현되지 않는다고 말한다.
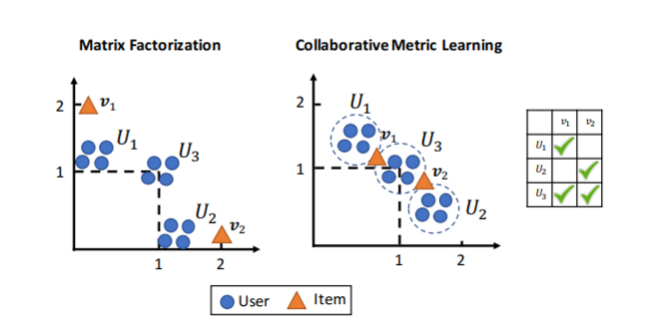
위의 latent vector들을 한 좌표평면에 모두 표현하면 u1-v1, u2-v2와 가까운 반면, 둘다 선호했던 u3는 둘다 멀어보인다는 것이다. 논문은 기존 MF 모델은 이처럼 두 가지 한계가 있다고 한다.
- MF 모델은 User 3 의 feedback을 적절하게 표현하지 못했다.
- latent vector은 user-user그리고 item-item 간의 유사도는 잘 나타내지 못했다.
반면 CML은 이런 상황에서 loss function에 의해서 v1, v2를 user한테 가깝게 당기게 될 것이다. 동시에 traingle inequality를 유지하기 위해 user-user item-item similarity역시 반영될 것이다.
위의 사진에서 보듯 user들은 좋아하는 아이템이 공유되므로 기존 MF 모델보다도 서로 가깝게 위치하게 될 것이다.
4. Experiments 생략
5. Conclusion
본 논문에서 우리는 새로운 CML이라는 논문을 소개했다. 이 모델은 user-item 관계뿐만 아니라 user-user/item-item similarity를 embedding space에 반영하였고, 그에 따른 regularization, feature fusion그리고 training technique을 소개했다.
CML은 다양한 추천 도메인에서 압도적인 accuracy를 달성할 수 있었다. Top-K recommendation task에서 off-the shelf, nearest neighbor, search algorithm, 을 통해 시간을 줄일 수 있었고, CML이 user의 디테일하고 밝혀지지 않은 선호까지 알아내는 것을 보여주었다.
Explicit feedback에서 implicit feedback으로 넘어오면서 Collaborative feedback은 rating을 예측하기 보다 user의 상대적인 선호도를 찾아내는 것으로 넘어갔다. Matrix factorization의 대안으로 우리는 CML 알고리즘으 이런 관계성을 직관적으로 찾아낼 수 있다고 본다.
이는 metric-based algorithm (예를 들어 kNN, K-means, svm)이 CF에 적용될 가능성을 시사하고 있다. 우리는 item feature만 대응했었지만, future work으로 user feature역시 사용할 수 있을 것이다.
논문 : https://www.cs.cornell.edu/~ylongqi/paper/HsiehYCLBE17.pdf
그외 참고 :
https://velog.io/@2chalsu/CMLCollaborative-Metric-Learning
'머신러닝,딥러닝' 카테고리의 다른 글
| conda에 gcc 설치하기 명령어 (0) | 2023.02.15 |
|---|---|
| kaggle tensorflow version 오류 -> 코랩가서 하기 (0) | 2023.02.03 |
| kaggle ~ RuntimeError: DGL requires tensorflow>=2.2.0 for the official DLPack support. 에러와 해결방법 (0) | 2023.02.01 |
| device cuda available code (0) | 2023.01.27 |
| [GNN 관련 논문] TransE: Translating Embeddings for Modeling Multi-relational Data 논문 리뷰 (0) | 2023.01.11 |
| 유클리드 거리 vs 제곱 유클리드 거리 (squared euclidean distance or SED) (0) | 2023.01.11 |
| dgl과 gpu를 사용할 때 에러가 날 경우 (0) | 2023.01.03 |
| Error : TypeError: 'tensorflow.python.framework.ops.EagerTensor' object is not callable 오류 원인 (0) | 2023.01.03 |